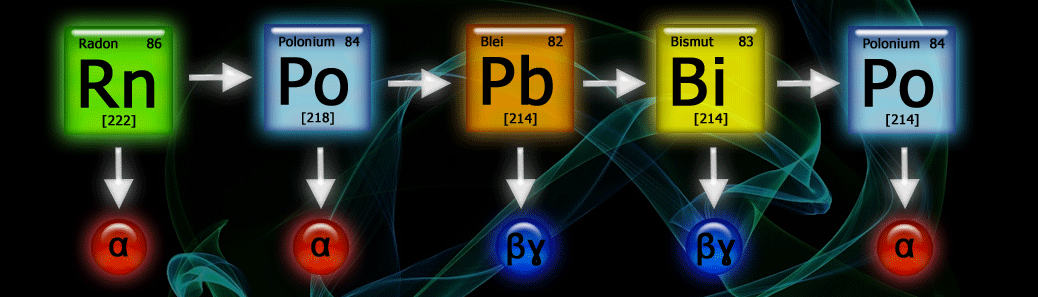
Determination of the Detection Efficiency of the Detector
To calculate the measurement quantity from the counts stored in the measurement data file, as shown in Equation 1 on the page „Prinzip der Messung von Radonfolgeprodukten“ the detection efficiency is required in addition to determining the air flow rate.
For the measurement of alpha radiation, the detection efficiency (η) consists of:
- the so-called geometry factor (ηGeo), and
- the filter collection efficiency (ηFilter).
The geometry factor is the ratio of the number of emitted alpha particles to the number of particles hitting the detector. This requires calculating the probability that an alpha particle emitted in any direction will reach the detector. For this calculation, the detector’s geometry, the source’s dimensions, and the distance between the detector and the filter are needed.
The calculation is somewhat complex and will not be discussed further here. The following table presents the values for various distances and filter diameters, assuming a square detector with an edge length of 2.5 mm (BPX 61 diode) and the central positioning of the filter above the detector:
Table 3: Geometry Factor for Filter Diameters from 5 mm to 8 mm at Various Distances Between Detector and Filter

(The values in Table 3 were calculated using an algorithm based on a Monte Carlo program and have a relative statistical uncertainty of approximately 1%. Intermediate values can be interpolated; significantly different dimensions can be requested via the comment field.)
When using the filter material MN 85/90, a filter collection efficiency of >99% can be assumed, and the detection efficiency can be equated with the geometry factor.
If, as described on the page „Luftansaugsystem“, a coffee filter is used, the filter collection efficiency is:
ηFilter ≈ 0.40.
Calculation of the Calibration Factor
To directly convert the measured pulses into the value of the measured quantity EEC or PAEC, a calibration factor can be defined, which is derived according to Equation 1 on the page “Principle of Measuring Radon Decay Products.”
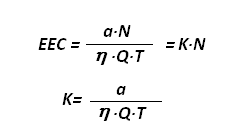
with:
- a: a constant depending on the units used,
- N: the number of counted pulses,
- η: the detection efficiency of alpha particles,
- Q: air flow rate (see the page “Air Intake System”),
- T: measurement time or counting interval duration.
If the units
- T in seconds (s),
- Q in liters per minute (l/min),
- EEC in Bq/m³
are used, then a = 13.2.
Example:
- Q = 0.25 l/min,
- η = 0.064,
- T = 3600 s.
Then K = 0.23.
Program Details
The integration of libraries for the peripheral devices RTC, LCD display, and SD card module will not be further explained here (refer to the Arduino reference).
The program’s functionality includes:
- Continuously monitoring the analog input to which the pulses are applied (see explanations on the page „Impulsmessung, Messwertverarbeitung, Datenspeicherung mit Arduino nano“) and registering a pulse when the set threshold is exceeded.
- Summing the registered pulses until the set measurement time elapses.
- Storing the pulse count together with the date and time after the set measurement time has elapsed.
- Optionally storing the value of the measured quantity EEC/PAEC calculated using the calibration factor.
In my program proposal (download available at the bottom of the page), both pulse counts and EEC values are stored. To do so, the calibration factor must be entered into the program.
The air flow rate is determined as described above. Unfortunately, the flow rate may change during the measurement due to dust accumulation on the filter. Therefore, the EEC values displayed on the screen and stored on the SD card should be considered as preliminary guidance. If necessary, the air flow rate should be corrected with a post-measurement after the measurement series is completed.
For precise evaluation, the stored pulse values should be used, and the EEC calculation should be performed using a spreadsheet program. For the program version with the thoron cycle, calculating the PAEC for thoron decay products is only possible via a spreadsheet.
Measurement Modes for Radon and Thoron Decay Product Analysis
For the measurements, I propose two program variants:
1. Continuous Measurement
The evaluation follows Equation 1. This approach determines the combined sum of radon and thoron decay products. However, thoron decay products typically contribute significantly less to this total. Therefore, the result can approximately be interpreted as the EEC/PAEC of radon decay products.
2. Quasi-Continuous Measurement with Alternating Pump Operation
This method allows for the separate determination of radon and thoron decay products by utilizing their specific decay characteristics and constants.
- Radon decay products decay almost completely within ~3 hours.
- Thoron decay products, primarily influenced by the nuclide Pb-212 (half-life ~10 hours, see Table 2), remain on the filter for a significantly longer time.
By implementing a collection pause of more than 3 hours, thoron decay products can be measured without interference from radon decay products. For the separate determination of radon decay products, the previously measured thoron product values can be used.
Measurement Cycle Example
I utilized the following cycle:
- Continuous filter exposure for 24 hours.
- Pump switched off for 12 hours.
- Pulse measurements conducted hourly.
Observational Example
The following graph illustrates changes in the activity of radon and thoron decay products on the measurement filter over two cycles, assuming constant values of EEC and C(Pb-212).
This setup ensures accurate assessment and differentiation between radon and thoron decay products by strategically exploiting their decay timelines.
Figure: Filter Activity of Radon and Thoron Decay Products in the Measurement Cycle (24-hour exposure, 12-hour pause), using the example values:, C(Pb-212) = 2 Bq/m³, EEC = 100 Bq/m³, Q = 0.25 l/min

Uncertainty of Measurement
The estimation of the uncertainty of measured values is just as important as determining the measured value itself. According to the definition, a measured value consists of an “estimate,” which is the value commonly referred to as the measured value, and its associated measurement uncertainty.
Here is an estimation of the relative measurement uncertainty achievable with the described DIY setup (basic standard uncertainty):
The estimation is again based on Equation 1. The following contributions to measurement uncertainty can be identified:
- Uncertainty in calibration factor: Variations due to imprecise calibration or environmental changes.
- Uncertainty in pulse count (N): Statistical fluctuations in detected pulses.
- Uncertainty in air flow rate (Q): Changes in the pump’s performance or dust accumulation on the filter.
- Uncertainty in measurement time (T): Inaccuracies in timing mechanisms.
- Detector efficiency (η): Variations due to the detector’s sensitivity to alpha particles.
These factors collectively contribute to the overall measurement uncertainty, which can be quantified using the propagation of uncertainty formula from Equation 1. The relative uncertainty provides a helpful insight into the reliability of the obtained results.
i: ηGeo
ii: ηFilter
iii: Q
iv: N
i.
The uncertainty of the geometry factor is due to the uncertainty in the measurement of the following parameters:
- Edge length of the active diode area (detector)
- Diameter of the filter
- Distance between detector and filter
The uncertainty for each of these parameters can be estimated at approximately 0.2 mm when a caliper is used for length measurement.
This results in a relative uncertainty of approximately σ(ηGeo) = ±15%.
ii.
The relative uncertainty of the filter collection efficiency, when using the filter material MN 85/90, is less than 1% and can therefore be considered negligible. However, when using coffee filters for testing purposes, the relative uncertainty is estimated to be σ(ηFilter) = ±15%.
iii.
The relative uncertainty in the determination of the air flow rate is primarily determined by measuring the time it takes for the soap bubble to travel between the markers. With an average time of 5 seconds and 5 repetitions of the measurement, I estimate the relative uncertainty to be approximately σ(Q) = 15%. If significant differences are observed between the measured values before and after a measurement period, these should also be considered when estimating the uncertainty. However, my experience shows that the air flow rate at Q = 0.25 l/min changed only marginally over a one-week measurement period. Based on previous experiences, I would assume a maximum uncertainty of σ(Q) = 20%.
iv.
Die Unsicherheit der Impulsmessung ist abhängig von der Impulszahl selbst und durch den stochastischen Charakter des Kernzerfalls bedingt. Die relative Unsicherheit ergibt sich dafür aus der sog. Poissonstatistik und beträgt

Example:
With N=100 follows σ(N=100)=10%.
The uncertainty in the pulse collection time can be completely disregarded.
Uncertainty of the Calibration Factor
This uncertainty arises from the individual contributions, which are added quadratically:
σ(K)={σ(Q)^2+σ(ηGeo)^2+σ(ηFilter)^2+σ(N)^2}^0.5
With the values mentioned above, the following uncertainties can be estimated for a measured pulse count of N = 100 (rounded values):
- When using the filter material MN 85/90 and no additional uncertainties due to air flow rate variations, σ(K) = 20%.
- When using the filter material MN 85/90 and additional uncertainties due to air flow rate changes during the measurement, σ(K) = 30%.
- When using a coffee filter and additional uncertainties in the air flow rate are expected, σ(K) = 60%.
These uncertainties may seem high when compared to other measurements, such as temperature. While lower uncertainties could be pursued, they would come at a disproportionately higher cost. It is also important to consider that the assessment of a room’s radon and thoron decay product load from these measurements can be influenced by daily and seasonal variations. Therefore, uncertainties of around 50% are acceptable for measuring radon decay products with a homemade device.
Quality Assurance in the Measurement of Radon and Thoron Decay Products
The mentioned uncertainties, according to the current assessment, align with practical conditions if we assume that:
- All pulses are counted.
- No electromagnetic interference (EMI) causes additional pulses.
The flow rate has been determined using the described methods.
The air flow rate should be checked again after the measurement is completed. For result calculations, the average between the initial and final values should be used. This is generally only recommended for the first measurements. Under nearly identical conditions regarding dust load, empirical values can be used. If significant differences occur, interpolated air flow rate values should be used for each individual measurement to achieve the uncertainties mentioned above.
Electromagnetic interference (EMI) should be checked by deliberately switching on large consumers near the measurement site and observing the impact on the displayed pulse count.
If the discriminator threshold is set too high and pulses are detected in the noise background, the pulse rate will be unreasonably high, which can easily be identified as noise.
To assess the plausibility of measurement values, the pulse count per hour and the EEC values listed in Table 4, using a device built according to the described construction plan, can serve as a reference. In areas without elevated radon potential, EEC values around 25 Bq/m³ (or less) can be expected in normal living spaces, while in basement rooms, values are typically around 50-100 Bq/m³.
Table 4 would typically show how pulse counts (per hour or other time intervals) are related to the calculated EEC values, with example parameters that affect the measurements such as air flow rate, calibration factors, or detector efficiency. These relationships help in understanding how variations in the pulse count correspond to specific radon or thoron decay product concentrations (EEC) in different environments, like basements or standard living spaces.
Table 4: Relationship between Measured Pulse Count and EEC Measurement Values using the following parameters:
η= 0.039, Q= 0.25 l/min, T= 3600 s, K= 0.38, a=13.2

Evaluation of Measurement Results
To evaluate the measurement results, they must be compared to a threshold or reference value. This is where the challenge arises, as the establishment of such thresholds or reference values is multifaceted. While this issue will not be explored in depth here, some brief explanations are provided:
Contrary to the argument on the homepage that measuring the decay products would be better than measuring radon as a gas for assessing exposure, reference values for the maximum allowable concentrations are based on the gas itself. This is ultimately due to the common practice of using passive detectors (so-called solid-state track detectors) for measurement.
EU radiation protection guidelines recommend that member states set reference values for maximum radon activity concentrations in homes no higher than 300 Bq/m³ (becquerels per cubic meter of air) (“Directive on basic safety standards for protection against the dangers arising from exposure to ionizing radiation”; Chapter VIII, Section 3; Article 74). In Germany, from October 2017, a reference value of 300 Bq/m³ will apply to living spaces. The Federal Office for Radiation Protection (BfS) recommends considering measures to reduce radon concentrations for values above 100 Bq/m³. Simple actions include regular ventilation of affected rooms and sealing doors to basement areas.
Interested parties can also refer to the corresponding pages of the BfS (Federal Office for Radiation Protection) and the BMUB (Federal Ministry for the Environment, Nature Conservation, Building and Nuclear Safety).
If one wishes to compare their radon decay product measurements with a reference value for the maximum radon concentration, a conversion must be made:
As described, the concentration of decay products is always lower than the radon concentration. The difference between radon gas and decay products is expressed through a so-called equilibrium factor; this is the ratio of the measurement quantity EEC to the radon concentration. For residential areas, an average equilibrium factor of around 0.5 is used. This means that to compare measurement values with reference values, the EEC decay product measurements must be multiplied by a factor of 2. The reference value of 300 Bq/m³ would be reached if the EEC value measured with your decay product detector was 150 Bq/m³.
Summary:
- To calculate the measurement quantity EEC or PAEC from the measured pulses, the pulse count must be multiplied by the calibration factor.
- The calibration factor requires knowledge of the air flow rate, measurement time, and detection efficiency, which is composed of the geometric factor and filter collection efficiency. To calculate the geometric factor, knowledge of the detector dimensions, filter diameter, and the distance between the detector and filter is necessary. Table 3 can be used for these determinations.
- The continuous measurement (constant exposure of the filter) and evaluation according to Equation 1 provides a sum determination of radon and thoron decay products. For separate determination of radon and thoron decay products, a periodic exposure of the filter with continuous pulse measurement is required.
- The key requirements for quality assurance include:
- Measuring the air flow rate and checking the tightness of the air intake system,
- Avoiding the registration of noise pulses, and
- Ensuring the reliable counting of all alpha particles that reach the detector (necessity for pulse shaping).
- The evaluated measurement values, multiplied by a factor of 2, are compared with the reference value of 300 Bq/m³ (radon gas concentration).
If these points are considered, you can start measuring with confidence, and I wish you much success, new insights, and not too high (realistic) measurement values.
Download Excel Table for Measurement Analysis
Berechnung der Radon und Thoronfolgeprodukte aus den Impuls-Messwerten
Download Arduino Sketch for Continuous Measurement:
Radonfolgeproduktmessung; kontinuierlich
Download Arduino Sketch for Discontinuous Measurement:
Radon- und Thoronfolgeproduktmessung; diskontinuierlich
Download mathematical basics of the used calculations