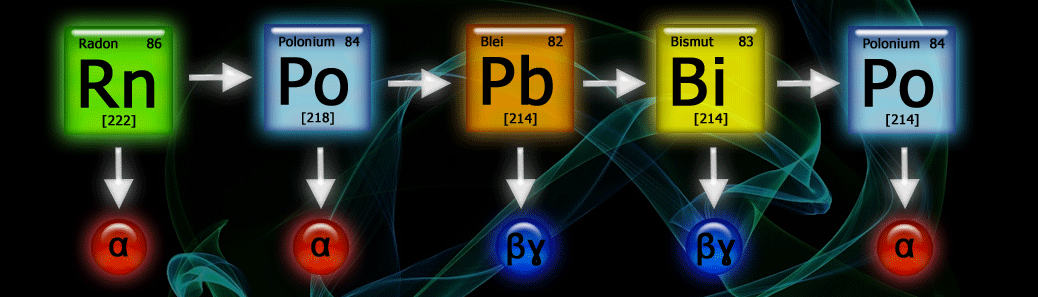
Bestimmung der Nachweiseffektivität des Detektors
Um aus den in der Messwertdatei gespeicherten Impulsen die Messgröße zu berechnen ist, wie Gleichung 1 der Seite „Prinzip der Messung von Radonfolgeprodukten“ zeigt, neben der Bestimmung des Luftdurchsatzes auch die Nachweiseffektivität erforderlich.
Bei der Messung von Alphastrahlung setzt sich die Nachweiseffektivität η zusammen aus
- dem sog. Geometriefaktor ηGeo und
- dem Filterabscheidegrad ηFilter;
η=ηGeo ∙ ηFilter.
Der Geometriefaktor ist das Verhältnis von der Anzahl emittierter Alphateilchen zu der Anzahl der auf den Detektor treffenden Teilchen. Man muss also berechnen, mit welcher Wahrscheinlichkeit ein in beliebiger Richtung emittiertes Alphateilchen den Detektor trifft. Dazu benötigt man die Geometrie des Detektors, die Abmessungen der Quelle und den Abstand zwischen Detektor und Filter. Die Berechnung ist nicht so ganz trivial und soll hier nicht weiter diskutiert werden. In folgender Tabelle sind die Werte für verschiedene Abstände und Filterdurchmesser dargestellt wobei ein quadratischer Detektor mit Kantenlänge 2.5 mm (Diode BPX 61)und die zentrale Positionierung des Filters über dem Detektor zugrunde gelegt wird:
Tabelle 3: Geometriefaktor für die Filterdurchmesser 5 mm bis 8 mm bei verschiedenen Abständen zwischen Detektor und Filter
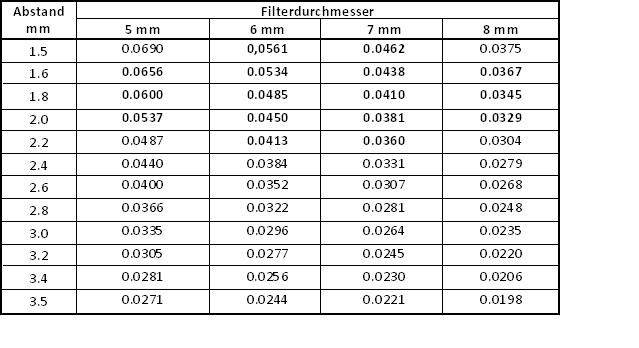
(Die Werte in Tabelle 3 sind mit einem Algorithmus auf der Grundlage eines Monte-Carlo-Programms berechnet und mit einer relativen statistischen Unsicherheit von ca. 1% behaftet. Zwischenwerte können interpoliert werden; stark abweichende Abmessungen können über das Kommentarfeld bei mir abgefragt werden)
Wenn das Filtermaterial MN 85/90 verwendet wird, kann man von einem Filterabscheidegrad > 99% ausgehen und die Nachweiseffektivität kann mit dem Geometriefaktor gleichgesetzt werden.
Wenn, wie in der Seite „Luftansaugsystem“ beschrieben, ein Kaffefilter verwendet wird, beträgt
ηFilter ≈ 0.40.
Berechnung des Kalibrierfaktors
Um die gemessenen Impulse direkt in den Wert der Messgröße EEC oder PAEC umzurechnen, kann man einen Kalibrierfaktor definieren, der sich entsprechend Gleichung 1 der Seite „Prinzip der Messung von Radonfolgeprodukten„ ergibt:
![]() (2)
(2)
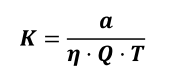 (3)
(3)
mit:
a: Konstante, die von den verwendeten Maßeinheiten abhängt,
N: Anzahl der gezählten Impulse,
η: Effektivität des Nachweises der Alphateilchen,
Q: Luftdurchsatz (siehe Seite „Luftansaugsystem“ ),
T: Messzeit bzw. Zeit des Zählintervalls.
Wenn die Maßeinheiten
- T in s (Sekunden) und
- Q in l/min (Liter/Minute)
- EEC in Bq/m3
verwendet werden, ist a=13.2.
Beispiel:
Q = 0.25 l/min,
η = 0.064,
T = 3600 s;
Dann ist K=0.23.
Zum Programm:
Die Einbindung der Bibliotheken für die peripheren Geräte RTC, LCD-Display und SD-Card-Modul soll hier nicht weiter beschrieben werden (siehe Arduino-Referenz).
Die Funktion des Programms besteht in:
- Ständiger Abfrage des Analogeingangs auf den die Impulse gelegt werden (siehe auch Erklärungen in der Seite „Impulsmessung, Messwertverarbeitung, Datenspeicherung mit Arduino nano“) und Registrierung als Impuls wenn der eingestellte Schwellwert überschritten wird;
- Summierung der registrierten Impulse bis zum Ablauf der eingestellten Messzeit;
- Speicherung der Impulszahl nach Ablauf der eingestellten Messzeit zusammen mit Datum und Uhrzeit und
- optionaler Speicherung des mit dem Kalibrierfaktors berechneten Wertes der Messgröße EEC/PAEC.
In meinem Programmvorschlag (Download am Ende der Seite ) ist die Speicherung sowohl von Impulszahlen als auch EEC-Werten vorgesehen. Dazu ist der Kalibrierfaktor in das Programm einzutragen.
Der Luftdurchsatz wird wie oben beschrieben bestimmt. Leider kann sich der Durchsatz infolge der Staubbeladung des Filters im Verlauf der Messung ändern. Deshalb sind die auf dem Display angezeigten und auf der SD-Karte gespeicherten EEC-Werte als vorläufige Orientierung zu betrachten. Evtl. muss der Wert für den Luftdurchsatz mit einer Nachmessung nach Beendigung der Messreihe korrigiert werden. Für eine exakte Auswertung sollten deshalb die gespeicherten Impulswerte verwendet werden und die Berechnung der EEC mit einem Tabellenkalkulationsprogramm durchgeführt werden. Für die Programmvariante mit Thoronzyklus ist die Auswertung der PAEC für Thoronfolgeprodukte ohnehin nur über die Tabellenkalkulation möglich.
Messmodi zur Radon- und Thoronfolgeproduktmessung
Für die Messungen schlage ich 2 Programmvarianten vor:
- Kontinuierliche Messung
- Quasikontinuierliche Messung mit alternierenden Pumpbetrieb
1.
Die Auswertung erfolgt nach Gleichung 1. Die kontinuierliche Messung ist eine Summenbestimmung von Radon- und Thoronfolgeprodukten. Meist sind Thoronfolgeprodukte jedoch mit wesentlich geringerem Anteil in dieser Summenbestimmung enthalten. Deshalb kann man das Ergebnis näherungsweise auch als EEC/PAEC von Radonfolgeprodukten interpretieren.
2.
Die quasikontinuierliche Messung dient zur separaten Bestimmung von Radon- und Thoronfolgeprodukten. Dafür werden die spezifischen Zerfallseigenschaften, Zerfallskonstanten, von Radon- und Thoronfolgeprodukten ausgenutzt. Radonfolgeprodukte sind nach ca. 3 h praktisch abgeklungen während Thoronzerfallsprodukte (das bestimmende Nuklid Pb-212 hat eine Hlabwertszeit von ca. 10 h, siehe Tabelle 2) wesentlich länger auf dem Filter vorhanden sind. Deshalb kann man mit einer Sammelpause von >3h die Thoronfolgeprodukte ohne Überlagerung durch Radonzerfallsprodukte messen. Für die separate Bestimmung der Radonfolgeprodukte wiederum kann man den Messwert der (ungestört gemessenen) Thoronfolgeprodukte verwenden. Dafür habe ich einen Messzyklus bestehend aus
- Filter kontinuierlich 24 Stunden beaufschlagen und
- Pumpe für 12 Stunden ausschalten
verwendet. Die Impulsmessung wird kontinuierlich im Stundenrythmus durchgeführt.
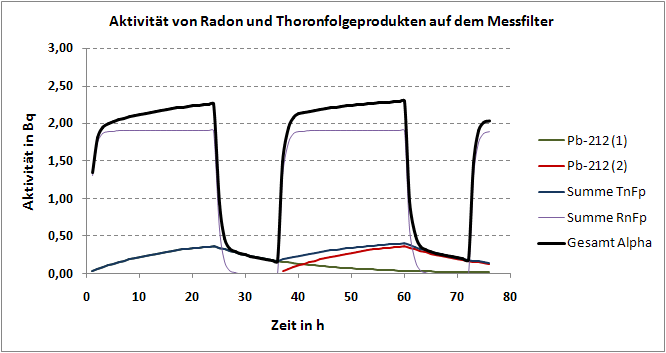
Die folgende Grafik zeigt am Beispiel, wie sich die Aktivität von Radon- und Thoronfolgeprodukten auf dem Messfilter während eines Zeitabschnitts von 2 Zyklen ändert (konstante Werte von EEC und C(Pb-212)).
Bild: Filteraktivität von Radon- und Thoronfolgeprodukten im Messzyklus 24 h Beaufschlagung 12 h Pause am Beispiel C(Pb-212)= 2 Bq/m3; EEC=100 Bq/m3; Q=0.25 l/
Messunsicherheit
Die Abschätzung der Unsicherheit von Messwerten ist genauso wichtig wie Ermittlung des Messwertes selbst. Lt. Definition besteht ein Messwert aus einem „Schätzwert“, das ist der Wert der gemeinhin als Messwert bezeichnet wird, und der zugeordneten Messunsicherheit.
Hier ist eine eine Abschätzung der relativen Messunsicherheit, die mit der beschriebenen Bastelversion erreicht werden kann (einfache Standardunsicherheit):
Grundlage der Abschätzung ist wieder Gleichung 1. Danach gibt es folgende Beiträge zur Messunsicherheit:
i: ηGeo
ii: ηFilter
iii: Q
iv: N
i.
Die Unsicherheit des Geometriefaktors ist bedingt durch die Unsicherheit der Messung der Parameter:
- Kantenlänge der aktiven Diodenfläche (Detektor),
- Durchmesser des Filters und
- Abstand Detektor Filter.
Die Unsicherheit für alle Parameter kann jeweils ca. 0.2 mm abgeschätzt werden wenn ein Messschieber zur Längenmessung verwendet wird.
Daraus resultiert eine relative Unsicherheit von ca. σ(ηGeo)=±15%.
ii.
Die relative Unsicherheit des Filterabscheidegrades beträgt bei Verwendung des Filtermaterials MN 85/90 weniger als 1% und damit praktisch zu vernachlässigen, wogegen bei der Verwendung von Kaffefilters zu Testzwecken mit einer relativen Unsicherheit von σ(ηFilter)=±15% abgeschätzt auszugehen wäre.
Die relative Unsicherheit der Bestimmung des Luftdurchsatzes wird im Wesentlichen durch die Messung der Zeit, die die Seifenblase zwischen den Markierungen benötigt, bestimmt. Bei im Mittel 5 Sekunden und 5 Wiederholungen der Messung schätze ich die relative Unsicherheit mit ca. σ(Q)=15% ab. Sollten sich bei der Messung des Luftdurchsatzes vor – und nach einer Messperiode deutliche Unterschiede zwischen den gemessenen Werten ergeben, sollte das ebenfalls bei der Abschätzung der Unsicherheit berücksichtigt werden. Meine Erfahrungen zeigten jedoch, dass sich Luftdurchsatz bei Q=0.25 l/min und einer Woche Messzeit nur geringfügig geändert hat. Als Maximum würde ich nach bisherigen Erfahrungen σ(Q)=20% annehmen.
iv.
Die Unsicherheit der Impulsmessung ist abhängig von der Impulszahl selbst und durch den stochastischen Charakter des Kernzerfalls bedingt. Die relative Unsicherheit ergibt sich dafür aus der sog. Poissonstatistik und beträgt
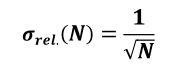 (4)
(4)
Beispiel:
Bei N=100 ist σ(N=100)=10%.
Die Unsicherheit der Impulssammelzeit kann man vollständig vernachlässigen.
Unsicherheit des Kalibrierfaktors
Diese ergibt sich aus den Enzelbeiträgen durch quadratische Addition :
σ(K)={σ(Q)^2+σ(ηGeo)^2+σ(ηFilter)^2+σ(N)^2}^0.5 (5)
Mit den o.g. Werten ergibt sich bei einer gemessenen Impulszahl N = 100 (gerundete Werte):
- wenn das Filtermaterial MN 85/90 verwendet wird und keine zusätzlichen Unsicherheiten im Luftdurchsatz zu befürchten sind σ(K)=20%,
- wenn das Filtermaterial MN 85/90 verwendet wird und zusätzliche Unsicherheiten infolge Änderungen des Luftdurchsatz während der Messung zu befürchten sind σ(K)=30%,
- wenn der Kaffefilter verwendet wird und zusätzliche Unsicherheiten im Luftdurchsatz zu befürchten sind σ(K)=60%.
Diese Unsicherheit erscheinen wahrscheinlich hoch, wenn man diese mit anderen Messungen wie z.B. Temperatur vergleicht. Man könnte zwar geringere Unsicherheiten anstreben, müsste das jedoch mit einem unverhältnismäßig höheren Aufwand bezahlen. Dabei muss man auch berücksichtigen, dass die Bewertung der Belastung eines Raumes mit Radon- und Thoronfolgeprodukten aus den Messungen auch von tages- und jahreszeitlich bedingten Änderungen beeinflusst wird. Unsicherheiten in der Größenordnung von 50% sind folglich für die Messung von Radonfolgeprodukten mit einem selbst gebauten Messgerät durchaus akzeptabel.
Qualitätssicherung bei der Messung von Radon- und Thoronfolgeprodukten
Die genannten Unsicherheiten entsprechen nach bisheriger Einschätzung den praktischen Gegebenheiten wenn man davon ausgehen kann,
- dass alle Impulse gezählt werden,
- keine EMV-bedingten Impulse auftreten und
- der Durchsatz mit den beschriebenen Mitteln bestimmt wurde.
Der Luftdurchsatz sollte nach Beendigung der Messung erneut kontrolliert werden. Für die Berechnung der Ergebnisse sollte dann der Mittelwert zwischen Anfangs- und Endwert verwendet werden. Das ist eigentlich nur bei den ersten Messungen anzuraten. Bei annähernd gleichen Bedingungen hinsichtlich der Staubbelastung kann man von den Erfahrungswerten ausgehen. Bei sehr große Differenzen sollten für jeden einzelnen Messwert interpolierte Werte für den Luftdurchsatz verwendet werden, um die o.g. Werte für die Messunsicherheit zu erreichen.
Die Einflüsse von EMV-Einstreuungen sollte man prüfen, indem große Verbraucher in der Nähe der Messstelle bewusst geschaltet werden und der Einfluss auf die angezeigte Impulszahl beobachtet wird.
Wenn die Diskriminatorschwelle zu hoch eingestellt ist und Impulse im Rauschuntergrund erfasst werden, ist die Impulsrate unplausibel hoch und kann damit leicht als Rauschen erkannt werden.
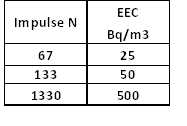
Zur Einschätzung der Plausibiltät von Messwerten können die in Tabelle 4 aufgeführten Wertepaare Impulszahl pro Stunde und Messgröße EEC am Beispiel eines nach dem hier beschriebenen Bauplan aufgebauten Gerätes dienen. In Regionen ohne erhöhtes Radonpotential sind in normal bewohnten Räumen EEC-Werte um 25 Bq/m3 (oder weniger) und in Kellerräumen eher 50 – 100 Bq/m3 zu erwarten.
Tabelle 4: Zusammenhang zwischen gemessener Impulszahl und Messgröße EEC am Beispiel mit den Parametern:
η= 0.039
Q= 0.25 l/min
T= 3600 s
K= 0.38
a=13.2
Bewertung der Messergebnisse
Zur Bewertung der Messwerte müssen diese zu einem Grenz- oder Richtwert in Beziehung gesetzt werden. Genau hier beginnt die Schwierigkeit. Die Festlegung von Grenz- oder Richtwerten ist aber sehr vielschichtig. Die Problematik soll hier nicht vertieft werden; hier nur einige kurze Erläuterungen:
Entgegen der Argumentation in der Startseite, dass für die Beurteilung der Belastung die Messung der Folgeprodukte besser wäre als die Messung von Radon als Gas, werden Richtwerte für maximal zu tolerierende Konzentrationen auf das Gas bezogen. Das ist letztendlich durch die gängige Praxis der Messung mit passiven Detektoren (sog. Festkörperspurdetektoren) bedingt.
Die EU-Grundnormen zum Strahlenschutz empfehlen den Mitgliedstaaten, Richtwerte für maximale Radon-Aktivitätskonzentrationen in Wohnungen nicht über 300 Bq/m^3 (Bequerel pro Kubikmeter Luft) festzulegen („Richtlinie zur Festlegung grundlegender Sicherheitsnormen für den Schutz vor den Gefahren einer Exposition gegenüber ionisierender Strahlung“; Kapitel VIII, Abschnitt 3; Artikel 74). In Deutschland wird ab Oktober 2017 ein Referenzwert von ebenfalls 300 Bq/m^3 in Aufenthaltsräumen gelten. Das Bundesamt für Strahlenschutz empfiehlt, schon bei Konzentrationen oberhalb von 100 Bq/m^3 über Maßnahmen zur Senkung der Radonkonzentration nachzudenken. Einfache Maßnahmen sind z.B. regelmäßiges Lüften der betreffenden Räume und Abdichtung von Türen zum Kellerraum.
Interessierte können sich auch auf den entsprechenden Seiten des BfS (Bundesamt für Strahlenschutz) und des BMUB (Bundesministerium für Umwelt, Naturschutz, Bau und Reaktorsicherheit) informieren.
Wenn man den Vergleich der eigenen Radonfolgeproduktmesswerte mit einem Richtwert für die maximale Radonkonzentration anstellen will, muss noch eine Umrechnung vorgenommen werden:
Wie beschrieben ist die Konzentration der Folgeprodukte immer geringer als die Radonkonzentration. Der Unterschied zwischen Radon-Gas und Folgeprodukten wird durch einen sog. Gleichgewichtsfaktor ausgedrückt; das ist das Verhältnis von der Messgröße EEC zur Radonkonzentration. Für Wohnräume kann man mit einem mittleren Gleichgewichtsfaktor von ca. 0.5 rechnen. D.h., dass man für den Vergleich von Mess- und Richtwerten die Messwerte für EEC Folgeprodukte noch mit dem Faktor 2 multiplizieren muss. Der Richtwert von 300 Bq/m^3 wäre damit erreicht, wenn der mit dem eigenen Folgeprodukt-Messgerät erhaltene Wert EEC=150 Bq/m^3 betragen würde.
Zusammenfassung:
- Um aus den gemessenen Impulsen die Messgröße EEC oder PAEC zu berechnen, muss die Impulszahl mit dem Kalibrierfaktor multipliziert werden.
- Zur Berechnung des Kalibrierfaktors benötigt man den Luftdurchsatz, die Messzeit und die Nachweiseffektivität, die sich wiederum aus dem Geometriefaktor und dem Filterabscheidegrad zusammensetzt.
- Für die Berechnung des Geometriefaktors ist die Kenntnis der Detektorabmessungen, des Filterdurchmessers und des Abstandes zwischen Detektor und Filter notwendig. Zur Bestimmung kann Tabelle 3 verwendet werden.
- Die kontinuierliche Messung (konstante Beaufschlagung des Filters) und Auswertung nach Gleichung 1 ist eine Summenbestimmung von Radon- und Thoronfolgeprodukten.
- Für die getrennte Bestimmung von Radon- und Thoronfolgeprodukten ist eine periodische Beaufschlagung des Filters bei ununterbrochener Messung der Impulse erforderlich.
- Die wichtigsten Erfordernisse zur Qualitätssicherung sind:
- Luftdurchsatz messen und Dichtheit des Luftansaugsystems prüfen,
- Vermeidung der Registrierung von Rauschimpulsen und
- sichere Zählung aller Alphateilchen, die den Detektor treffen (Notwendigkeit der Impulsformung)
- Bewertung der mit dem Faktor 2 multiplizierten Messwerte durch Vergleich mit dem Richtwert von 300 Bq/m^3 (Radon-Gas-Konzentration).
Wenn diese Punkte beachtet werden, kann munter „losgemessen“ werden, wozu ich viel Erfolg, neue Erkenntnisse und nicht zu hohe (reale) Messwerte wünsche.
Download Exceltabelle zur Auswertung der Messungen
(am 18.09.2017 aktualisiert; Fehler bei der Thoronzerfallsproduktberechnung beseitigt):
Berechnung der Radon und Thoronfolgeprodukte aus den Impuls-Messwerten
Download Arduino-Sketch für die kontinuierliche Messung:
Radonfolgeproduktmessung; kontinuierlich
Download Arduino-Sketch für die diskontinuierliche Messung:
Radon- und Thoronfolgeproduktmessung; diskontinuierlich
Bitte unbedingt auch auf meine Hinweise auf der Startseite achten.
Für Mitteilungen zu Problemen oder für Hinweise und Anfragen bitte das Kommentarfeld benutzen.